yukicoder No.453 製薬会社

問題はこちら
No.453 製薬会社 - yukicoder

線形計画法とか知らないけど数学で殴るだけ

製品Aをxkg、製品Bをykgつくるとすると、問題は
3/4*x+2/7*y≦C
1/4*x+5/7*y≦D
x,y≧0
の条件下で1000*x+2000*yを最大化する問題
厳密な証明を書くのが面倒くさくなったので、図でごまかす
下図は3/4*x+2/7*y=C…(1)を青線、1/4*x+5/7*y=D…(2)を赤線としたものであり、C,Dの値によって3パターン用意した。
黄色の領域が上で述べた条件を満たす範囲になる。



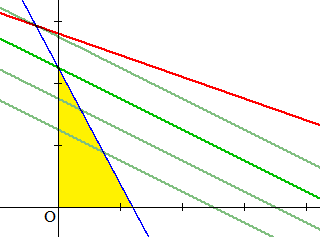
緑線が1000x+2000y=sのsを動かしたものであり、黄色部分と共有点を持つような最大のsを求めるのが問題。
この図を眺めると(1)(2)の交点が
・第１象限（軸上含む）ならその点で
・x<0なら(1)上のx=0の点で
・y<0なら(2)上のy=0の点で
それぞれ最大値を取ることが分かる
（厳密な証明は次の2つを示せば良い。「2つの材料をどちらもちょうど使い切る割当てが存在するならそのとき最大」「存在しないならばどちらか一方のみを作ったとき最大」。どちらもそれ以外に最大値があるとして背理法から従う）

(1)(2)の連立方程式を解くと
x=4/13*(5C-2D)
y=7/13*(-C+3D)
が得られる。
ということで求めるべき答えは
・5C-2D≧0かつ-C+3D≧0のとき、x,yは上で求めた通りであり1000x+2000y=(3C+17D)*2000/13
・5C-2D<0のとき、x=0,y=7/2*Cであり1000x+2000y=7000C
・-C+3D<0のとき、x=4*D,y=0であり1000x+2000y=4000D

int main(){
	double c,d;
	scanf("%lf%lf",&c,&d);
	if(-c+3*d<0)printf("%f",4000*d);
	else if(5*c-2*d<0)printf("%f",7000*c);
	else printf("%f",(3*c+17*d)*2000/13);
	return 0;
}

ぎゅ

a;main(float b){a=scanf("%d%f",&a,&b)>printf("%f",a>3*b?b*4e3:a<.4*b?a*7e3:(6*a+34*b)/.013);}

93B

perlなら最短狙えるとおもってこれを投げた

<>=~$";print$`<$'*.4?$`*7e3:$'*3<$`?$'*4e3:($`*6+$'*34)/.013

プロに一瞬で抜かれた

<>=~$";print$`<$'*.4?$`*7:$'*3<$`?$'*4:($`*6+$'*34)/13,e3

というかなんだこれは。perl自由すぎるだろ