問題はこちら
No.306 さいたま2008 - yukicoder
元ネタは高校入試の問題らしいけど、むしろ中学入試の難問としてよくみる問題のように思う
そういうわけで中学数学くらい丁寧に証明してみよう。
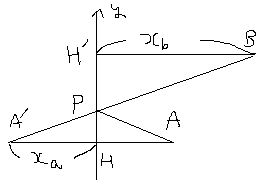
Aをy軸に対称に移してA'としAA'とy軸の交点をHとする。
AH=A'H、∠AHP=∠A'HP=90°より△APHと△A'PHは合同になるのでAP=A'P
よってA'P+PBを小さくすれば良い
これは明らかにPが線分A'B上にあるとき最短。そのようにPを取る
Bを通りy軸に平行な直線とy軸の交点をH'とすると
∠BPH'=∠PA'H、∠BH'P=∠PHA=90°となるので△BPH'と△PA'Hは相似
よってHP:H'B=xa:xb
即ちPは(0,ya)と(0,yb)をxa:xbに内分する点となる
int main(){ int xa,ya,xb,yb; scanf("%d%d%d%d",&xa,&ya,&xb,&yb); printf("%f",1.0*(yb*xa+ya*xb)/(xa+xb)); //内分点の公式を知らなければ、素直に //HP=HH'*xa/(xa+xb)からya+(yb-ya)*xa/(xa+xb)とすれば良い return 0; }
a,b,c;main(d){a=scanf("%d%d%d%d",&a,&b,&c,&d)>printf("%f",1.*(d*a+b*c)/(a+c));}
79B