yukicoder No.526 フィボナッチ数列の第N項をMで割った余りを求める

問題はこちら
No.526 フィボナッチ数列の第N項をMで割った余りを求める - yukicoder

普段より丁寧めに解説。

一般的なフィボナッチ数列とはindexが1つずれていることに注意

・漸化式に従って再帰的に計算する
詳細は省くがO(φ^N)となりTLE

fib(n,m){
	if(n==1)return 0;
	if(n==2)return 1;
	return (fib(n-1,m)+fib(n-2,m))%m;
}
main(){
	int n,m;
	scanf("%d %d",&n,&m);
	printf("%d",fib(n,m));
}

・メモ化する
上のコードで何が問題かを考える。
例えばfib(10,m)を呼ぶと、その中でfib(9,m)とfib(8,m)が呼ばれる。
するとfib(9,m)の中でfib(8,m)とfib(7,m)が呼ばれ…となり、nが小さくなる毎にfib(n,m)が呼ばれる回数は指数関数的に大きくなってしまう。
そこで、「1度計算したことがある値はその結果を残しておき、2度目以降には計算しない」ようにすることを考える。
これがメモ化と呼ばれるテクニック

int memo[5000010];
fib(n,m){
	if(n==1)return 0;
	if(n==2)return 1;
	if(memo[n])return memo[n];
	memo[n]=(fib(n-1,m)+fib(n-2,m))%m;
	return memo[n];
}
main(){
	int n,m;
	scanf("%d %d",&n,&m);
	printf("%d",fib(n,m));
}

各nに対しfib(n,m)は高々1回しか計算されないので、O(N)で求めることができる

・DP
問題はこれで既に解けたわけだが、上のコードではmemo[5000010]という大きめの配列をとっており、メモリ効率が悪い。
例えばN=10^8でメモリ制限が256MBだとMLEになってしまう（int型で長さ10^8だと(4*10^8)B≒400MB以上必要）
これを解決するのがDPと呼ばれるテクニック。
よく使われる表現として「メモ化はトップダウン、DPはボトムアップ」というものがある。
今回の問題に関して言えばメモ化では「fib(10,m)を求めたい→fib(9,m)を求めたい→fib(8,m)を求めたい→……」と上から降りていったが、DPでは「…→fib(8,m)を求めた→fib(9,m)を求めた→fib(10,m)を求めた」というように下から昇っていく。
まずはわかりやすく、今まで通り大きな配列をとるDP

main(){
	int n,m,fib[5000010];
	fib[1]=0;
	fib[2]=1;
	scanf("%d%d",&n,&m);
	for(int i=3;i<=n;i++)fib[i]=(fib[i-1]+fib[i-2])%m;
	printf("%d",fib[n]);
}

ループの部分をよく見ると、fib[i]を求めるのにはfib[i-1]とfib[i-2]しか使っていない。
つまりそれより古い情報は捨ててしまって問題ないので、このことを使って次のように配列を使わずに書ける

main(){
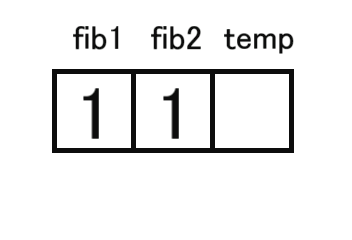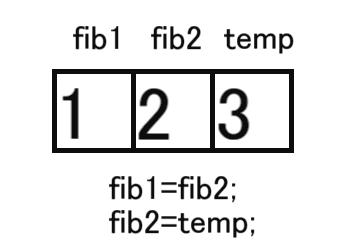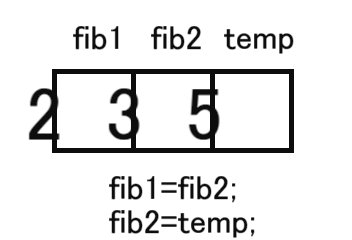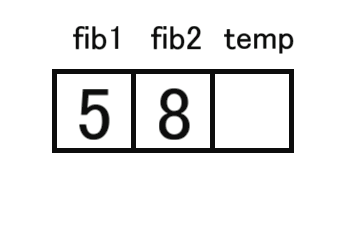
	int n,m,fib1,fib2,temp;
	fib1=0;
	fib2=1;
	scanf("%d%d",&n,&m);
	for(int i=3;i<=n;i++){
		temp=(fib2+fib1)%m;
		fib1=fib2;
		fib2=temp;
	}
	printf("%d",fib2);
}

Q.どういうこと？
A.これみて
f:id:sugarknri:20170619101629g:plain

・メモ化再帰vsDP
じゃあメモ化再帰よりDPの方がいいのか！→そうとは限らない
例えば
$a_1=a_2=1\\ a_n=a_{\lfloor 2\sqrt n\rfloor}+a_{\lfloor \sqrt n\rfloor}\ \ (n\geq 3)$
という漸化式で与えられる数列の第N項を求めることを考えてみると、（Nが十分大きいときは）DPよりメモ化再帰の方がよい。
（なぜならNと2√Nの間の値は、a_Nを計算するために一度も使わないので）
この辺の話は難しいので興味がある人は各自調べること

－－－これ以降は中級者以上向け－－－

・行列累乗
「K項線形漸化式の第N項は行列累乗を用いることでO(K^3 logN)で求まる」というテクニックがある
$a_n=p_1a_{n-1}+...+p_ka_{n-k}$ という漸化式で数式が与えられるとき、

$\begin{pmatrix} p_1 & \cdots & \cdots & p_k \\ 1 & & 0 & 0 \\ & \ddots & & \vdots \\ 0 & & 1 & 0 \end{pmatrix} \begin{pmatrix} a_{n-1}\\ \vdots\\ \vdots\\ a_{n-k} \end{pmatrix} = \begin{pmatrix} a_n\\ \vdots\\ \vdots\\ a_{n-k+1} \end{pmatrix}$
が任意のnに対して成立するので、このことを使って

$\begin{pmatrix} p_1 & \cdots & \cdots & p_k \\ 1 & & 0 & 0 \\ & \ddots & & \vdots \\ 0 & & 1 & 0 \end{pmatrix} ^{n-k} \begin{pmatrix} a_k \\ \vdots\\ \vdots\\ a_1 \end{pmatrix} = \begin{pmatrix} a_n\\ \vdots\\ \vdots\\ a_{n-k+1} \end{pmatrix}$

と見ることができる。
（K項じゃなくてK+1項じゃん→オーダーを見るときには関係ないから許して）
行列同士の1回の掛け算にO(K^3)かかるので、繰り返し二乗法を使うことでO(K^3 logN)で計算することができる

さらに、この形の行列（コンパニオン行列）に限っては通称"きたまさ法"により(K^2 logN)で求めることができるらしい（まだ理解していない）
とはいえ今回はK=2なのであまり関係ない。

普通の行列累乗による実装を以下に示す

#define ll long long
ll fibm(ll n,int m){
	//0,1,1,1をn乗して2番目を返す
	//一般の行列累乗は面倒だったのでadhoc
	ll aa=0,bb=1,cc=1,dd=1;
	ll a=1,b=0,c=0,d=1;
	ll ta,tb,tc,td;
	while(n){
		if(n%2){
			ta=aa*a+bb*c;
			tb=aa*b+bb*d;
			tc=cc*a+dd*c;
			td=cc*b+dd*d;
			a=ta%m;b=tb%m;c=tc%m;d=td%m;
		}
		ta=aa*aa+bb*cc;
		tb=aa*bb+bb*dd;
		tc=cc*aa+dd*cc;
		td=cc*bb+dd*dd;
		aa=ta%m;bb=tb%m;cc=tc%m;dd=td%m;
		n/=2;
	}
	return b;
}

n,m;
main(){
	scanf("%d%d",&n,&m);
	printf("%d",fibm(n-1,m));
}

ゴルフはといえば、DP解をぎゅっとするだけ

long x,i,t,m;main(y){for(scanf("%d%d",&i,&m);--i;x=y,y=t%m)t=x+y;printf("%d",x);}

81B